Süleyman Cengizci, Ömür Uğur, A Stabilized FEM Formulation with Discontinuity-Capturing for Solving Burgers’ Type Equations at High Reynolds Numbers, Applied Mathematics and Computation, 442: 127705 (April 2023, December 2022).
Abstract
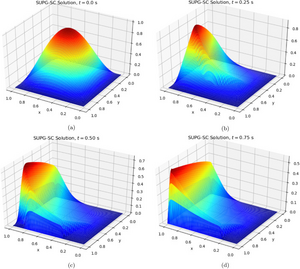
This computational study is concerned with the numerical solutions of Burgers’-type equations at high Reynolds numbers. The high Reynolds numbers drive the nonlinearity to play an essential role and the equations to become more convection-dominated, which causes the solutions obtained with the standard numerical methods to involve spurious oscillations. To overcome this challenge, the Galerkin finite element formulation is stabilized by using the streamline-upwind/Petrov-Galerkin method. The stabilized formulation is further supplemented with YZβ shock-capturing to achieve better solution profiles around strong gradients. The nonlinear equation systems arising from the space and time discretizations are solved by using the Newton–Raphson (N–R) method at each time step. The resulting linearized equation systems are solved with the BiCGStab technique combined with ILU preconditioning at each N–R iteration. A comprehensive set of test examples is provided to demonstrate the robustness of the proposed formulation and the techniques used.
Keywords: Burgers’ equation, High Reynolds number, Finite elements, SUPG, YZβ shock-capturing