Alev Meral, M.Sc.
Department of Financial Mathematics
August 2013
Supervisor: Ömür Uğur (Institute of Applied Mathematics, Middle East Technical University, Ankara)
Abstract
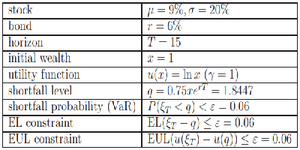
In this thesis, we search for optimal portfolio strategies in the presence of various risk measure that are common in financial applications. Particularly, we deal with the static optimization problem with respect to Value at Risk, Expected Loss and Expected Utility Loss measures. To do so, under the Black-Scholes model for the financial market, Martingale method is applied to give closed-form solutions for the optimal terminal wealth, then via representation problem the optimal portfolio strategies are achieved. We compare the performances of these measures on the terminal wealth and optimal strategies of such constrained investors. Finally, we present some numerical results to compare them in several respects to give light to further studies.
Keywords: Portfolio Optimization, Value at Risk, Expected Loss, Expected Utility Loss, Black-Scholes Model, Martingale Method, Risk Constraints