Süleyman Cengizci, Ömür Uğur, A Comparative and Illustrative Study for Solving Singularly Perturbed Problems with Two Parameters, TWMS Journal of Applied and Engineering Mathematics, 14(2): pp. 520 - 536 (April 2024, August 2022).
Abstract
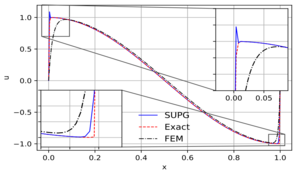
This computational study concerns approximate solutions of singularly perturbed one-dimensional boundary-value problems having perturbed convection and diffusion terms. Such kinds of problems take different stands depending on the perturbation parameters. Typically, when the problem is convection-dominated, classical discretization methods suffer from numerical instability issues. Therefore, standard methods require special treatment in convection dominance. To this end, in this work, the standard Galerkin finite element method (GFEM) is stabilized with the streamline-upwind/Petrov–Galerkin (SUPG) formulation. Beyond that, an asymptotic approach, called the successive complementary expansion method (SCEM), is also proposed. Two test examples are provided to evaluate and compare the proposed methods’ performances for various values of the convection and diffusion parameters.
Keywords: asymptotic expansion, finite elements, singularly perturbed, stabilization, two parameters