Hatice Anar, M.Sc.
Department of Financial Mathematics
August 2008
Supervisor: Ömür Uğur (Institute of Applied Mathematics, Middle East Technical University, Ankara)
Co-supervisor: Azize Hayfavi (Institute of Applied Mathematics, Middle East Technical University, Ankara)
Abstract
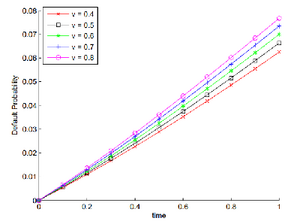
In this thesis, the structural model in credit risk and the credit derivatives is studied under both Black-Scholes setting and Variance Gamma (VG) setting. Using a Variance Gamma process, the distribution of the firm value process becomes asymmetric and leptokurtic. Also, the jump structure of VG processes allows random default times of the reference entities. Among structural models, the most emphasis is made on the Black-Cox model by building a relation between the survival probabilities of the Black-Cox model and the value of a binary down and out barrier option. The survival probabilities under VG setting are calculated via a Partial Integro Differential Equation (PIDE). Some applications of binary down and out barrier options, default probabilities and Credit Default Swap par spreads are also illustrated in this study.
Keywords: Lévy process, variance gamma process, credit risk, structural model, survival probability, credit default swap, barrier option, partial-integro differential equation