İsmail Hakkı Gökgöz, M.Sc.
Department of Financial Mathematics
September 2012
Supervisor: Ömür Uğur (Institute of Applied Mathematics, Middle East Technical University, Ankara)
Co-supervisor: Yeliz Yolcu Okur (Institute of Applied Mathematics, Middle East Technical University, Ankara)
Abstract
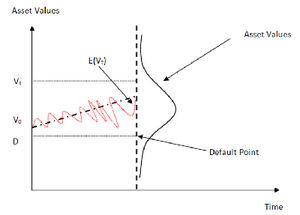
Credit risk measurement and management has great importance in credit market. Credit derivative products are the major hedging instruments in this market and credit default swap contracts (CDSs) are the most common type of these instruments. As observed in credit crunch (credit crisis) that has started from the United States and expanded all over the world, especially crisis of Iceland, CDS premiums (prices) are better indicative of credit risk than credit ratings. Therefore, CDSs are important indicators for credit risk of an obligor and thus these products should be understood by market participants well enough. In this thesis, initially, advanced credit risk models firsts, the structural (firm value) models, Merton Model and Black-Cox constant barrier model, and the intensity-based (reduced-form) models, Jarrow-Turnbull and Cox models, are studied. For each credit risk model studied, survival probabilities are calculated. After explaining the basic structure of a single name CDS contract, by the help of the general pricing formula of CDS that result from the equality of in and out cash flows of these contracts, CDS price for each structural models (Merton model and Black-Cox constant barrier model) and CDS price for general type of intensity based models are obtained. Before the conclusion, default intensities are approximately estimated from the distribution functions of default under two basic structural models; Merton and Black-Cox constant barrier. Finally, we conclude our work with some inferences and proposals.
Keywords: Credit risk, credit derivatives, single name credit default swap, credit crunch, structural model, intensity-based model, Merton model, Black-Cox constant barrier model, Jarrow-Turnbull model, Cox model, default intensity, survival probability, probability of default